 % K. v, |5 u( Q5 `
% K. v, |5 u( Q5 `��(sh��)�W(xu��)�Ҍ�(du��)�ݾ���̽����������ݵ���ϣ�D�r(sh��)��,�������¾�������������Փ�ݾ����Ќ�(du��)�����ݾ������|(zh��)����Ԕ��(x��)��ӑՓ,�����Ǻ����Ĕ�(sh��)�W(xu��)�҂�Ҳ�ѵ����ݾ��Q(ch��ng)�顰�������ݾ���,��������l(f��)�F(xi��n)�Ƚ��ݾ����䌍(sh��)�ǰ����µ��ώ����r(n��ng),�������������^�������Ĺ�������
ʲô�ǰ������ݾ���,��������һ�������@��һ�c(di��n)�D(zhu��n)��(d��ng)���L(zh��ng)�U,����һֻС�x(ch��ng)�����U����������ȥ����(d��ng)�L(zh��ng)�U�����D(zhu��n)��(d��ng)�ĕr(sh��)��С�x(ch��ng)��(hu��)����܉�E���ǰ������ݾ�,���������ݾ��ķ��̌�(xi��)�ɘO����(bi��o)��ʽ���� �� = a�ȡ�

�������ݾ��������S̎��Ҋ(ji��n),�������ڵ����C(j��)��,��늙C(j��)����(d��ng)�D(zhu��n)�P(p��n)�ϵij�Ƭ�����D(zhu��n)��(d��ng)������һ�lֱ��܉����������Ȧ�Ƅ�(d��ng)�ij��^�ڳ�Ƭ�����µĿ̲۾��ǰ������ݾ�,��ͬ��,���Ʉ��ٱP(p��n)��C(j��)���a(ch��n)����(l��i)�ıP(p��n)������Ҳ�ǰ������ݾ����Π���ݾ����ᔏ���^����ȥҲ�ǰ������ݾ�,�����B�p�x�C(j��)��Ҳ�а������ݾ����](m��i),��һ��ęC(j��)е�p�x�C(j��)����һ��(g��)݆����݆���D(zhu��n)�ĕr(sh��)���Á�(l��i)����(d��ng)�p�x��^ֱ���\(y��n)��(d��ng),���@��(g��)݆��݆�����ǰѰ������ݾ���һ���ֽ�(j��ng)�^(gu��)��(du��)�Q(ch��ng)�õ���,��
һ��(g��)����Ȥ�������ǣ��ڰ������ݾ��������,����Ҏ(gu��)����������ȷ�һ��(g��)����Ǧ�,�����E���£�
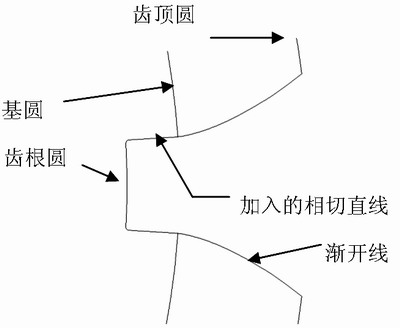
1�����Ƚǵ�һ߅�c�O�S�غ�,����c(di��n)�cԭ�c(di��n)O�غ�2,�����L(zh��ng)�ǵ���һ߅�c�������ݾ�����A3����Ҏ(gu��)���ȷ�OA�õ����ȷ��c(di��n)B��,��C��4,���քe��O(sh��)B��,��OC����돽��O��A�Į�(hu��)�A���ݾ���B,��C5,������(j��) ��=a�� �����C��OB��OC���ȷ֦�
��(d��ng)Ȼ,��ֻ���ó�Ҏ(gu��)�ǟo(w��)����(hu��)���������ݾ���,�������҂���ɲ���?f��)?d��n)���P(gu��n)�ڳ�Ҏ(gu��)���ȷ�����Dz����ܵ��C���ʹ˱��Ƶ���
��һ�N�������ݾ������u�_(k��i)��,����(d��ng)һ���K������һ�����@�ϻ�Ó�r(sh��),�������һ�l�u�쾀���S�����������Լ��ĝu�_(k��i)��,����һ�l�](m��i)�Џ��Եļ�(x��)�K�@��һ��(g��)���A��,�����_(k��i)�K�ӵ�һ�˲���ֱ��ʹ�K���c�A��ʼ�K����,���K�Ӷ��c(di��n)��܉�E���LjA�ĝu�_(k��i)��,��

�c�������ݾ���ȣ��u�_(k��i)�����ճ������г���(ch��ng)�ęC(j��)��(hu��)�ƺ�Ҫ��һ�c(di��n),�����м�(x��)����߀���ܰl(f��)�F(xi��n)����ۙ�E,�������ؙ���һЩֲ���~���݆�����ǝu�_(k��i)�����䌍(sh��)��߀�ڙC(j��)е�O(sh��)���аl(f��)�]����Ҫ������,���C(j��)е�O(sh��)�����ڂ���(d��ng)���X݆��,���ͻ��S���u�_(k��i)������Ӱ������ 1694 ��,������(gu��)�W(xu��)�߾�ӑՓ�˰ѝu�_(k��i)�������X݆�X�εĿ�����,�� 1765 �꣬�W����(du��)�����ϵ�һ��(du��)�X݆�X�����������ʰ돽����������λ�õ��P(gu��n)ϵ�M(j��n)����Ӌ(j��)��,���J(r��n)��u�_(k��i)���ஔ(d��ng)�m�������X݆���X��,���c�����X����ȣ��u�_(k��i)���X�ξ��Ђ���(d��ng)ƽ��(w��n),����݆���ľ����S��һ���İ��b�`��ȵȃ�(y��u)�c(di��n),��Ŀǰ���I(y��)�Нu�_(k��i)���X݆���V����(y��ng)�ã�ռ�������X݆�Ј�(ch��ng)�� 90% ����,��
�u�_(k��i)���X݆
�������(ch��ng)�����ݾ��������������ġ����Ƚ��ݾ�,���������ց�(l��i)Դ��һ��(g��)�����Ĕ�(sh��)�W(xu��)��(w��n)�}��ԇ�ҳ�һ�l�������������c(di��n)̎��ʸ���c�о��ĊA�Ǟ鶨ֵ,���@һ��(w��n)�}��K�� 1683 �걻�ѿ�����Q,��ʹ��һ�c(di��n)��(ji��n)�ε��e�ֺ͵ѿ���������(bi��o)ϵ���҂���������֪���Ƚ������ĘO����(bi��o)���̣��� = e a�� ,�������ڷ����г��F(xi��n)��ָ��(sh��)����(sh��),���@һ�ݾ�Ҳ���Q(ch��ng)�錦(du��)��(sh��)�ݾ�,��
�Ƚ��ݾ�߀�cһ��������Ȥζ�����}���P(gu��n)����ֻС���քe��һ��(g��)��߅�����ε����c(di��n)���l(f��)������ͬ���ٶ����,����(d��ng)����?c��)����������������r(sh��),������(hu��)����܉�E���ǵȽ��ݾ���һ��(g��)���ٱ�ע�����Ȥ�F(xi��n)����,�������������ޕr(sh��)�g��(n��i)����,����������֮ǰ�ѽ�(j��ng)���������@�˟o(w��)��(sh��)Ȧ!

�Ƚ��ݾ�
�Ƚ��ݾ������S����Ȥ�Ĕ�(sh��)�W(xu��)���|(zh��)��������(sh��)�W(xu��)���Ÿ�������Ŭ�����ǵȽ��ݾ���һ��(g��)���۽z,������(du��)�Ƚ��ݾ��M(j��n)�����S���о�,���l(f��)�F(xi��n)�Ƚ������ڷ��ݡ���u����,����������,���ȱ����Ŵ�ȵ�׃�Q����Ȼ��ԭ�ȵĵȽ���������(du��)���@Щ���|(zh��)��Ŭ���е�ʮ���@Ӡ,���Q���ѵȽ����������Լ���Ĺ־�,��߀������һ��Ԓ��Eadem mutata resurgo.���@��Ԓ�и��N��ͬ�ķ��g�汾�������ǡ��vȻ��׃,����Ȼ���ҡ���Ҳ��һЩ�汾�ķ��g�(l��i)�ơ���׃֮��,���Ҍ�ԭ�؏�(f��)��������ǻ������Ǟ������Ĺ���Ĺ���Ҳ�S���Ļ�ˮƽ����,��Ҳ�S�������韩,�����oĹ���ϵ�̵ĈD���Ǻ������P(gu��n)�İ������ݾ�����Ŭ������Ȫ��֪,������Ҫ�����Ŀ�ˡ�

�Ƚnj�(du��)��(sh��)�ݾ��ij��˲�Ŭ��߀�д���Ȼ,�,��������������Ƚǵ����ԣ��Ƚ��ݾ�����Ȼ�����Ҋ(ji��n)���ݾ�,�����տ��ĺ�����һЩֲ��ķN���ڻ��P(p��n)�����г����������ǵȽ�����,���@��ÿ�w�N���ܵ���?ch��)������N�����������L(zh��ng)�ص��������ÿ����_(d��)����С��ͬ�r(sh��)��(d��ng)�����L(zh��ng)��r(sh��)���Ա����Π׃,��ާ�(l��i)ֲ�������һЩֲ������~Ҳ�����Ɍ�(du��)��(sh��)�������Π�,��

���տ��Ļ��P(p��n)���ܿ����Ƚ��ݾ���

��(du��)��(sh��)�����Π����ѿ
����ֲ���,����(d��ng)���Ҳ�в��ٵȽ��ݾ�,���W�^�ݵ��ݚ��������ǵȽ��ݾ����@�������W�^�������L(zh��ng)�r(sh��)��(n��i)Ȧ�c��Ȧ����ʯ���|(zh��)��������һ��ֵ��ɵ�,��ͬ����������~(y��)�ı���Ҳ�nj�(du��)��(sh��)�ݾ����Π�,������(gu��)����W(xu��)��,�������x(ch��ng)ӛ������ -����•����������(j��ng)ע���֩��Y(ji��)���ľW(w��ng)��Ҳ�Ќ�(du��)��(sh��)�ݾ����](m��i),����(du��)�����dȤ��l(f��),���ڡ�֩���һ�����������ˌ�(zhu��n)�T(m��n)��һƪ��ӑՓ��(du��)��(sh��)�ݾ��Ĕ�(sh��)�W(xu��)���|(zh��)������(du��)��Ȼ���Ӱ�,����������(du��)��(sh��)�ݾ����@��(g��)���־��Ƿ�������푵�,�������˂��l(f��)�F(xi��n)���w�����c�����P(p��n)��Ҳ����������(du��)��(sh��)�ݾ���܉�E�Ƅ�(d��ng),��
���Ǻͽ���(l��i)���y��ϵ���,�����ϵ����Ӷ��������ˡ������ČW(xu��)���^�y(c��)�l(f��)�F(xi��n),���u�������Ƶ������Π��c�Ƚ��ݾ�ʮ������,���y��ϵ���Ĵ����۾��ǃAб�Ȟ� 12�� �ĵȽ��ݾ���

����֮��,����(sh��)�W(xu��)�҂�߀�ҳ��˸��N���ι֠�ķ������ݾ�,������O����(bi��o)���� r 2 = �� �������B�i�ݾ��������dz�Ҋ(ji��n)��һ֧,�����nj�(du��)�Q(ch��ng)�ă�֧,������֮����ǚW���ݾ������Ѓɂ�(g��)����,�����᠖��һ����Ʒ�����Դ˞����}��,��

�W������
��(sh��)�W(xu��)������˵�?z��)�?��i)�ݾ��������ں���һ��(g��)��(sh��)�W(xu��)���Ƿ����ţ�Ƶĺ�(ji��n)�εķ������ǿ����Ƿ���������������ݾ�,�������������֞�ʲô��(du��)�ݾ����Ъ�(d��)���,���@�����������Y(ji��)���ǘӣ����Σ��Լ���e�ĺ��C֧����һ��,�,����ݾ�����(zh��n)��(y��u)�ŵ�Ҏ(gu��)�ɣ��o(w��)��һ����һ�����˞�֮�V��,��
; T0 a# L. y N) C a+ k3 K! w5 v1 ~9 ]
http://www.guokr.com/article/67148/

| �gӭ���R �C(j��)е��^(q��) (http://97307.cn/) | Powered by Discuz! X3.4 |